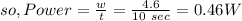Question

A robotic rover on Mars finds a spherical rock with a diameter of 10 centimeters​ [cm]. The rover picks up the rock and lifts it 20 centimeters​ [cm] straight up. The rock has a specific gravity of 4.75. The gravitational acceleration on Mars is 3.7 meters per second squared ​[m divided by s squared​]. If the​ robot's lifting arm has an efficiency of 40​% and required 10 seconds​ [s] to raise the rock 20 centimeters​ [cm], how much power in units of watts​ [W] did the arm​ use?

Answer 1

Power = 0.46 W

Step-by-step explanation:

Given data:

distance by which rock lift up is 20 cm

specific gravity of rocks is 4.75

Gravitational acceleration on mars is 3.7 m/sec

Efficiency 40%

we know that specific gravity of rocks

`S.G = (\rho_(rock))/(\rho_(water))`

`4.75* 1000  =\rho_(rock)`

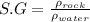
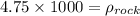
we know
`density = ( mass)/(volume)`

`mass_(rock) = 4.75* 1000  {(4)/(3) \pi ((0.1)/(2))^2} = 2.48 kg`

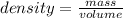
work done is
`W = (mgh)/(efficiency)`

`w = (2.48* 3.7* 0.2)/(0.4)`

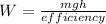
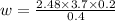
w = 4.6 j

`so, Power = (w)/(t) = (4.6)/(10\ sec) = 0.46 W`