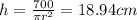Question

A microwaveable cup-of-soup package needs to be constructed in the shape of cylinder to hold 700 cubic centimeters of soup. The sides and bottom of the container will be made of styrofoam costing 0.02 cents per square centimeter. The top will be made of glued paper, costing 0.09 cents per square centimeter. Find the dimensions for the package that will minimize production cost.

Answer 1

r = 3.43 cm

h=18.94 cm

Explanation:

The volume of the cylinder is:

`V=\pi r^(2)h=700cm^(3)`

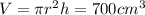
where r is the radius of the circular base and h is the height of the cylinder.

The cost of the side of the cylinder is:

`(0.02)2\pi rh`

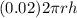
The cost ot the bottom of the container is:

`(0.02)\pi r^(2)`

The cost ot the top of the container is:

`(0.09)\pi r^(2)`

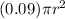
Then, the total cost of the container is:

`C=(0.02)2\pi rh+(0.02)\pi r^(2)+(0.09)\pi  r^(2) \\C=\pi r(0.04h+0.02r+0.09r)\\C=\pi r(0.04h+0.11r)`

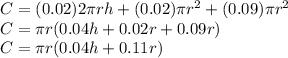
From the volume, you could solve for one variable and substituting in the cost equation:

`h=(700)/(\pi r^(2))\\C=\pi r(0.04((700)/(\pi r^(2)))+0.11r)`

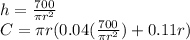
In order to minimize this fuction you need to calculate the derivative respect to r:

`(dC)/(dr) =(dC)/(dr)[(28)/(r)+0.11\pi    r^(2)]\\(dC)/(dr) =-(28)/(r^(2) )+0.22\pi  r`

The critical points of the function are obtained when dC/dr=0:

`-(28)/(r^(2))+0.22\pi  r=0\\0.22\pi r=(28)/(r^(2) )\\r^(3)= (28)/(0.22\pi ) \\r=3.43 cm`

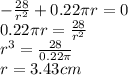
To evaluate if this critical point is a minimum, you should get the second derivative:

`(d^(2) C)/(dr^(2) ) =(28)/(r^(3) )+0.22\pi \\`

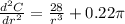
For the critical point r = 3.43 cm, the second derivative is positive, which means that the critical point is a minimum.

Then, the dimensions for the package tht will minimize product cost are:

r = 3.43 cm

`h=(700)/(\pi r^(2)  ) =18.94cm`