Answer:
Acceleration,

Step-by-step explanation:
It is given that,
Time period of revolution of the moon,
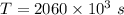
If the distance from the center of the moon to the surface of the planet is,
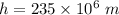
The radius of the planet,
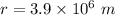
Let a is the moon's radial acceleration. Mathematically, it is given by :
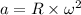 , R is the radius of orbit
, R is the radius of orbit
Since,
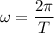
The radius of orbit is,

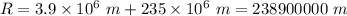
So,
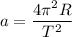
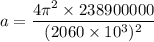

Hence, this is the required solution for the radial acceleration of the moon.