Answer:3.75 ft/s
Step-by-step explanation:
Given
Length of ladder(L)=40 feet
base of ladder moves at a rate of 5 ft/sec
Bottom of ladder from wall(x)=24 feet
let horizontal distance be x and vertical distance be y
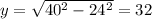
therefore
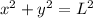 from Pythagoras
from Pythagoras
differentiate
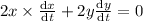
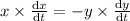
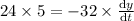
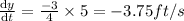
negative sign indicates height is decreasing