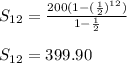Question

HELP ASAP PLEASE!!! 20 POINTS!!

What is the sum of the first 12 terms of the geometric series 200+100+50+25+...?

Give the answer to the nearest hundredth.

Use the formula Sn = a1(1−rn) / 1−r

Answer 1

Answer:
`S_(12)=399.90`

Explanation:

You know that the formula to find the sum of a finite geometric series is:

`S_n=(a_1(1-r^n))/(1-r)`

Where
`n` is the number of terms,
`a_1` is the first term and
`r` is the common ratio (
`r\\eq 1`).

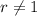The steps to find the sum of the first 12 terms of the given geometric serie, are:

1. Find the common ratio "r". By definition:

`r=(a_2)/(a_1)`

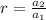
Then:

`r=(100)/(200)\\\\r=(1)/(2)`

2. Finally, knowing that:

`a_1=200\\\\n=12`

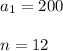
You must substitute values into the formula.

Then you get:

`S_(12)=(200(1-((1)/(2))^(12)))/(1-(1)/(2))\\\\S_(12)=399.90`