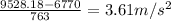Answer:
a.x component of acceleration of craft=
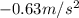
b.y component of acceleration of craft=
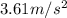
Step-by-step explanation:
We are given that two engines are turned on for 763 s.
x component of initial velocity of craft=
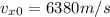
y component of initial velocity of craft=
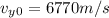
After firing,
x component of displacement of craft=
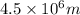
y component of displacement of craft=
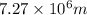
We know that velocity=
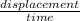
x component of final velocity of craft=
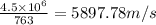
y component of final velocity of craft=
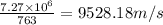
We know that acceleration =
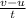
a.x component of acceleration of craft=
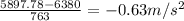
b.y component of acceleration of craft=