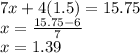Question

At a concession​ stand, seve hot dog (x )hot dog(s) and four hamburger (x )hamburger(s) cost ​$15.75; four hot dog (x )hot dog(s) and seven hamburger (x )hamburger(s) cost ​$17.2517.25. Find the cost of one hot dog and the cost of one hamburger.

Answer 1

Cost of one hot dog: $1.39 (rounded to the nearest hundredth)

Cost of one hambuger: $1.51 (rounded to the nearest hundredth)

Explanation:

Let x and y be the cost of one hot dog and the cost of one hamburger, respectively. With the information given, a system of equations is obtained:

`7x + 4y=15.75\\4x+7y=17.25`

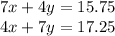
There are a lot of methods to solve a system like this, let's try the substitution method:

The first step is solving one of the equation for one of the variables, let's solve x for the first equation:

`x=(15.75-4y)/(7)`

Then, this value is substituted in the second equation and solved for the other variable:

`4((17.75-4y)/(7))+7y=17.25\\(71)/(7)-(16y)/(7)+7y=17.25\\- (16y)/(7)+ 7y=17.25-(71)/(7)  \\(33)/(7)y=(199)/(28)\\  y=(199(7))/(28(33))\\ y=199/132=1.51\\`

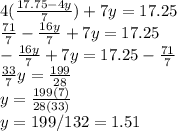
Finally, the value of y is substituted in any of the equations and solved for x:

`7x+4(1.5)=15.75\\x=(15.75-6)/(7) \\x=1.39`