Question

Assume that the business makes a profit with probability 0.8 in the first year. For each year thereafter, the business makes a profit with probability 0.9 if it made a profit in the previous year, and with probability 0.2 if it did not make a profit in the previous year. What is the probability that the business makes a profit in exactly two of its first three years?

Answer 1

The probability that the business makes a profit in exactly two of its first three years is 0.628.

Explanation:

Given : Assume that the business makes a profit with probability 0.8 in the first year. For each year thereafter, the business makes a profit with probability 0.9 if it made a profit in the previous year, and with probability 0.2 if it did not make a profit in the previous year.

To find : What is the probability that the business makes a profit in exactly two of its first three years?

Solution :

Let X be the event that the business makes profit.

Y be the event that the business doesn't .

The business makes a profit with probability 0.8 in the first year.

For each year thereafter, the business makes a profit with probability 0.9.

It did not make a profit in the previous year is 0.2.

According to question,

The business makes a profit in exactly two of its first three years which is given by, XXY, XYX, YXX

So,

`P(XXY)=0.8* 0.9* (1-0.2)`

`P(XXY)=0.8* 0.9* 0.8`

`P(XXY)=0.576`

`P(XYX)=0.8* (1-0.9)* 0.2`

`P(XYX)=0.8* 0.1* 0.2`

`P(XYX)=0.016`

`P(YXX)=(1-0.8)* 0.9* 0.2`

`P(YXX)=0.2* 0.9* 0.2`

`P(YXX)=0.036`

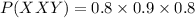
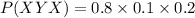
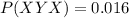
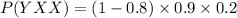
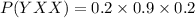
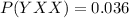
The probability that the business makes a profit in exactly two of its first three years is given by,

P= P(XXY)+P(XYX)+P(YXX)

P= 0.576+0.016+0.036

P= 0.628

Therefore, The probability that the business makes a profit in exactly two of its first three years is 0.628.

= 0.272