Question

A train moving at a constant speed of 50.0 km/h moves east for 45.0 min, then in a direction 45.0° east of due north for 10.0 min, and then west for 55.0 min. What is the average velocity of the train during this run? (Let the +x-axis point towards the east and the +y-axis point towards the north.)l

Answer 1

3.47km/h with a direction of 67.8 degrees north of west.

Step-by-step explanation:

First we need to calculate the displacement on the X axis, so:

`d_(x1)=50.0km/h*45min((1h)/(60min))=37.5km\\d_(x2)=50.0km/h*10min((1h)/(60min))*cos(45^o)=5.90km\\d_(x1)=-50.0km/h*55.0min((1h)/(60min))=45.8km\\D_x=37.5+5.90-45.8=-2.4km`

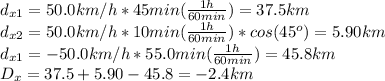
then on the Y axis:

`D_y=50.0km/h*10min((1h)/(60min))*sin(45^o)=5.90km`

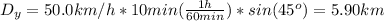
The magnitud of the displacement is given by:

`D=√(D_x^2+D_y^2) \\D=6.37km`

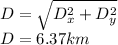
and the angle:

`\alpha =arctg((5.90)/(2.41))=67.8^o`

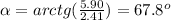
that is 67.8 degrees north of west.

`v=(D)/(t)\\v=(6.37km)/(110min*(1h)/(60min))\\v=3.47km/h`