Question

Edison Research gathered exit poll results from several sources for the Wisconsin recall election of Scott Walker. They found that 56% of the respondents voted in favor of Scott Walker. Additionally, they estimated that of those who did vote in favor for Scott Walker, 36% had a college degree, while 43% of those who voted against Scott Walker had a college degree. Suppose we randomly sampled a person who participated in the exit poll and found that he had a college degree. What is the probability that he voted in favor of Scott Walker?

Answer 1

Answer: Our required probability is 0.515.

Explanation:

Since we have given that

Probability that the respondents voted in favor of Scot Walker P(F) = 56%

Probability that the respondent voted in not favor of Scot Walker = 100-56 = P(F')=44%

Probability of those who did vote in favor had a college degree = 36% = P(C|F)

Probability of those who did vote against had a college degree = 44% = P(C|F')

So, we will use "Conditional Probability":

probability that he voted in favor of Scott Walker given that they had a college degree is given by

`P(F|C)=(0.56* 0.36)/(0.56* 0.36+0.44* 0.43)\\\\P(F|C)=0.515`

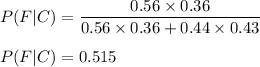
Hence, our required probability is 0.515.