Question

Find the volume of the largest rectangular box in the first octant with three faces in the coordinate planes and one vertex in the plane x + 2y + 3z = 12.

Answer 1

Explanation:

`x + 2y + 3z = 12`

`z=(12-x-2y)/(3)`

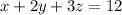
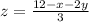
Volume =
`V=f(x,y) = xy((12-x-2y)/(3) )`

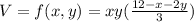
find partial derivatives using product rule

`f_x =(y)/(3) (12-2x-2y)\\f_y = (x)/(3) (12-x-4y)`

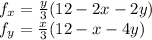
i.e.

Using maximum for partial derivatives, we equate first partial derivative to 0.

y=0 or x+y =6

x=0 or x+4y =12

Simplify to get y =2, x = 4

thus critical points are (4,2) (6,0) (0,3)

Of these D the II derivative test gives

D<0 only for (4,2)

Hence maximum volume is when x=4, y=2, z= 4/3

Max volume is = 4(2)(4/3) = 32/3