Question

Applying the functions to derive desired values Suppose you get a job offer from one of your dream companies and they are paying you within the range you would want your salary to be. Lets take this amount to be $45,000 per year. You are confident that working in this company would help you grow and charter a career path that you would like to pursue. You are curious to know that if your salary increases at the rate of 9.0% per year, how many years would it take to double your salary?

Answer 1

It will double his salary every 8.04 years

Step-by-step explanation:

Using the future value of a lump sum formula we solve for time at which 45,000 principal becomes 90,000:

`Principal \: (1+ r)^(time) = Amount`

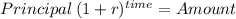
Principal: 45,000

time n

rate 0.09000

Amount: 90,000

`45000 \: (1+ 0.09)^(n) = 90,000`

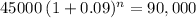
to solve for n we use logartihmics properties:

n = 8.043231727 = 8.04 years