Question

A suspicious-looking man runs as fast as he can along a moving sidewalk from one end to the other, taking 2.90 s. Then security agents appear and the man runs as fast as he can back along the sidewalk to his starting point, taking 10.7 s. What is the ratio of the man's running speed to the sidewalk's speed (running speed / sidewalk speed)?

Answer 1

68:39

Step-by-step explanation:

We have to find the ratio of the man's running speed to the sidewalk's speed.

Let running speed of man=x

Sidewalk's speed=y

When man running in the same direction as side walk is moving.

Then, total speed=x+y

Time=2.9 s

When a man running in opposite direction as the side walk is moving.

Then, total speed =x-y

Time =10.7 s

Distance traveled in both cases remain same.

Suppose , d is the distance from one end to another end.

`Distance=speed* time`

`(x+y)* 2.9=(x-y)* 10.7`

`2.9x+2.9y=10.7x-10.7y`

`10.7y+2.9y=10.7x-2.9x`

`13.6y=7.8 x`

`(x)/(y)=(13.6)/(7.8)`

`(x)/(y)=(68)/(39)`

`x:y=68:39`

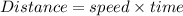
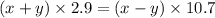
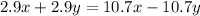
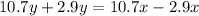
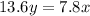
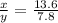
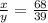
Hence, the ratio of the man's running speed to the sidewalk's speed =68:39