Question

You decide you want to be a millionaire. You deposit $50,000 in an investment account that earns 9% per year. The money in the account will be distributed to you whenever the total reaches $1,000,000. If you are 27 now, how old will you be when you get the money (rounded to the nearest year)?

(Hint: to know how old you will be, you need to know for how long your money should be invested in)

(A) 49 years
(B) 53 years
(C) 62 years
(D) 66 years

Answer 1

Answer: 35 years

Step-by-step explanation:

`A=P(1+(r)/(n))^(nt)`

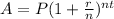
Where,

A - the ending amount,

P - the beginning amount (or "principal")

r - the interest rate (expressed as a decimal)

n - the number of compounding a year

t - the total number of years

n=1, t=?, P = $50,000, r=0.09, A= $1,000,000

Therefore,

`1,000,000=50,000(1+(0.09)/(1))^(t)`

`1,000,000=50,000(1.09)^(t)`

`20=(1.09)^(t)`

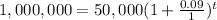
Taking log on both sides

log(20) = t log(1.09)

1.30103 = 0.0374264979 t

t = 34.7622

So answer is 35 years.