Question

On August 2nd, 1988, a US District Court judge imposed a fine on the city of Yonkers, New York, for defying a federal court order involving housing desegregation.

Suppose the city of Yonkers is offered two alternative fines by the judge.
(i) Penalty A: 1 million dollars on August 2 and the fine increases by 10 million dollars each day thereafter.
(ii) Penalty B: 1 cent on August 2 and the fine doubles each day thereafter.
(a) If t represents the number of days after August 2, express the fine incurred as a function of t under
Penalty A:
A(t)= __________ dollars
Penalty B:
B(t)= __________ dollars
(b) Assuming your formulas in part (a) hold for t≥0, is there a time such that the fines incurred under both penalties are equal?

Answer 1

a)

A(t) = 1,000,000 + 10,000,000t

B(t)= 0.01 +0.02t

b) No.

Explanation:

a) Penalty A: 1 million dollars on August 2 and the fine increases by 10 million dollars each day thereafter.

If t represents the number of days after August 2,

A(t) = 1,000,000 + 10,000,000t

Penalty B: 1 cent on August 2 and the fine doubles each day thereafter.

A(t) = 0.01 + 2t(0.01) = 0.01 + 0.02t

b) Assuming your formulas in part (a) hold for t≥0, is there a time such that the fines incurred under both penalties are equal?

To solve this, we would have to equal both formulas and solve for t.

`1,000,000 + 10,000,000t=0.01+0.02t\\9,999,999.98t=-999,999.99`

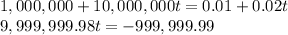
By taking a look at this equation, we see that when we solve for t, t will be a negative number. Since the formulas are valid for t≥0, we can conclude that there won't be a time such that the fines are equal.