Question

A ball is dropped from rest at point O. After falling for some time, it passes by a window of height 3.3 m and it does so in 0.27 s. The ball accelerates all the way down; let vA be its speed as it passes the window’s top A and vB its speed as it passes the window’s bottom B. Calculate the speed vA at which the ball passes the window’s top.

Answer 1

Speed at which the ball passes the window’s top = 10.89 m/s

Step-by-step explanation:

Height of window = 3.3 m

Time took to cover window = 0.27 s

Initial velocity, u = 0m/s

We have equation of motion s = ut + 0.5at²

For the top of window (position A)

`s_A=0* t_A+0.5* 9.81t_A^2\\\\s_A=4.905t_A^2`

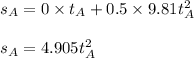
For the bottom of window (position B)

`s_B=0* t_B+0.5* 9.81t_B^2\\\\s_A=4.905t_B^2`

`\texttt{Height of window=}s_B-s_A=3.3\\\\4.905t_B^2-4.905t_A^2=3.3\\\\t_B^2-t_A^2=0.673`

We also have

`t_B-t_A=0.27`

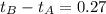
Solving

`t_B=0.27+t_A\\\\(0.27+t_A)^2-t_A^2=0.673\\\\t_A^2+0.54t_A+0.0729-t_A^2=0.673\\\\t_A=1.11s\\\\t_B=0.27+1.11=1.38s`

So after 1.11 seconds ball reaches at top of window,

We have equation of motion v = u + at

`v_A=0+9.81* 1.11=10.89m/s`

Speed at which the ball passes the window’s top = 10.89 m/s