Answer:
Minimum time = 6.177 min
Step-by-step explanation:
We assume a reference system with the positive x-axis (from left to right) and also a positive y-axis (from bottom to top)
According to this system the velocity vector of the river and the hunter are :
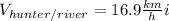
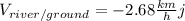
The velocity vector of the hunter relative to the ground is the sum of the previously mentioned velocities
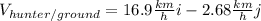
This means that,for example,in an hour the hunter moves 16.9 km in the positive x direction and 2.68 km in the negative y direction
We are looking for a displacement of 1.74 km in the x direction ⇒ We will use only the ''i'' component of the velocity

We multiply the time in hours by 60 to obtain the time in minutes
time T = 6.177 min