Question

Two current-carrying wires are parallel to each other. The current in one is increased by a factor of 2 , the current in the other is increased by a factor of 3 , and the distance between the wires is decreased by a factor of 13 . What is the change in the force between the wires?\

Answer 1

The new force
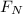`F_N` will be
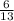`(6)/(13)` times the old force F. The change then will be
`\Delta F=-(7)/(13)F`

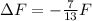
Step-by-step explanation:

The force between two current-carrying parallel wires is calculated with the formula:

`F=(\mu_0I_1I_2\Delta L)/(2\pi r)`

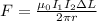
where r is the distance between them,
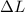`\Delta L` a portion of length of the wires we consider,
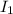`I_1` and
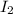`I_2` their current intensity and
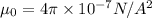`\mu_0=4\pi*10^(-7)N/A^2` the vacuum permeability.

If the current in one wire is increased by a factor of 2, the current in the other is increased by a factor of 3 , and the distance between the wires is decreased by a factor of 13, then we would have a new situation N where (considering the previous variables as an initial situation):

`I_(N1)=2I_1\\I_(N2)=3I_2\\r_N=13r\\`

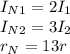
And the force then will be:

`F_N=(\mu_0I_(N1)I_(N2)\Delta L)/(2\pi r_N)=(\mu_02I_13I_2\Delta L)/(2\pi 13r)=(6(\mu_0I_1I_2\Delta L))/(13(2\pi r))=(6)/(13)F`

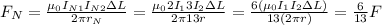
So the change will be:

`\Delta F=F_N-F=(6)/(13) F-F=((6)/(13) -1)F=-(7)/(13)F`