Option 2
ANSWER:
The Standard deviation of (7, 9, 10, 11, 13) is 2.
SOLUTION:
Given, data set is (7, 9, 10, 11, 13)
Standard deviation
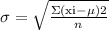
Where,
 is element of data set
is element of data set
 is mean of data set
is mean of data set
n is total number observations.
Now, mean

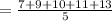
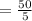
= 10
So, the mean of data set is 10.
Now, standard deviation
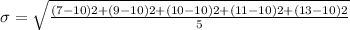

So, the standard deviation is 2.
Hence, the second option is right, i.e. standard deviation is 2.