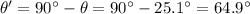Question

A bomber is flying horizontally over level terrain at a speed of 280 m/s relative to the ground and at an altitude of 3.50 km. (a) The bombardier releases one bomb. How far does the bomb travel horizontally between its release and its impact on the ground? Ignore the effects of air resistance. km (b) Firing from the people on the ground suddenly incapacitates the bombardier before he can call, "Bombs away!" Consequently, the pilot maintains the plane's original course, altitude, and speed through a storm of flak. Where is the plane relative to the bomb's point of impact when the bomb hits the ground? behind the bomb ahead of the bomb directly above the bomb (c) The plane has a telescopic bombsight set so that the bomb hits the target seen in the sight at the moment of release. At what angle from the vertical was the bombsight set?

Answer 1

(a) 7.48 km

The bomb follows a parabolic motion, where:

- The horizontal motion is a uniform motion with constant horizontal velocity

- The vertical motion is a free-fall motion (uniformly accelerated motion with constant acceleration,
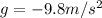`g=-9.8 m/s^2`, acceleration of gravity)

First of all, we analyze the vertical motion of the bomb in order to find the time of flight. The vertical displacement is given by:

`h=ut+(1)/(2)gt^2`

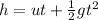
where

h = -3.50 km = -3500 m is the vertical displacement

u = 0 is the initial vertical velocity

t is the time of flight

Solving for t,

`t=\sqrt{(2h)/(g)}=\sqrt{(2(-3500))/((-9.8))}=26.7 s`

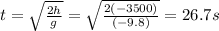
So, the bomb reaches the ground after 26.7 s.

Now we analyze the horizontal motion. We know that the horizontal velocity of the bomb is constant, and it is equal to the initial horizontal velocity of the plane:

`v_x = 280 m/s`

So, the horizontal distance travelled by the bomb before reaching the ground is

`d=v_x t = (280)(26.7)=7476 m = 7.48 km`

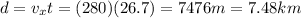
(b) Directly above the bomb

In this part, we are interested in the motion of the plane.

We know that the plane mantains a constant horizontal velocity of

`v_x = 280 m/s`

Therefore, the distance the plane travels before the bomb reaches the ground is

`d=v_x t = (280)(26.7)=7476 m = 7.48 km`

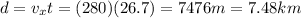
which is exactly the same distance travelled by the bomb: therefore, the plane is directly above the bomb.

(c)
`64.9^(\circ)`

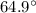
To find the angle at which the bombsight was before the bomb was dropped, we can just keep in mind that the horizontal distance travelled and the vertical displacement of the bomb are the sides of a right triangle, therefore the angle is given by

`tan \theta = (h)/(d)`

where

h = -3.50 km is the vertical displacement

d = 7.48 km is the horizontal distance travelled

Substituting,

`\theta = tan^(-1) ((-3.50)/(7.48))=-25.1^(\circ)`

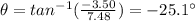
This is the angle below the horizontal: if we want to get the angle from the vertical, we do

`\theta' = 90^(\circ)-\theta=90^(\circ)-25.1^(\circ)=64.9^(\circ)`

Answer 2

(a)7.48331 Km

(b) Directly above the tomb

(c) 12.53 degrees

Step-by-step explanation:

Given that the distance is 3.5 Km, converted to meters we obtain 3500 m

Using the formula

`s=0.5gt^(2)` where s is the distance and t is time, taking acceleration due to gravity as 9.8 then

`3500 = 0.5*9.8*t^(2)`

t = 26.72 sec

We know that speed=distance/time hence to get the distance in part (a)

Distance=Speed*time

280 *26.72 = 7483.31 m converted to Km we obtain 7.48331 Km

(b)directly above the bomb

(c)
`tan \theta = \frac {3500}{7483.31}`

`\theta = 12.53^(o)`