Question

An airline has a policy of booking as many as 23 persons on an airplane that can seat only 22. ​(Past studies have revealed that only 85.0​% of the booked passengers actually arrive for the​ flight.) Find the probability that if the airline books 23 ​persons, not enough seats will be available. Is it unlikely for such an overbooking to​ occur?

Answer 1

The probability that the airline books 23 ​people is 0.024. We can consider that overbooking is something unlikely to occur.

Explanation:

This is binomial experiment so we can use the probability fuction of a binomial distribution:

P(x)=
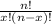`(n!)/(x!(n-x)!)`·pˣ·(1-p)ⁿ⁻ˣ

whrere:

p: is the probability of a passenger arrive for the flight (0.85)

n: number of experiments

Hence;

P(x=23)=
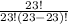`(23!)/(23!(23-23)!)`·(0.85)²³·(1-0.85)²³⁻²³

P(x=23)=(0.85)²³=0.024