Answer:
1/2, 3
Explanation:
This is a pretty involved problem, so I'm going to start by laying out two facts that our going to help us get there.
- The Fundamental Theorem of Algebra tells us that any polynomial has as many zeroes as its degree. Our function f(x) has a degree of 4, so we'll have 4 zeroes. Also,
- Complex zeroes come in pairs. Specifically, they come in conjugate pairs. If -2i is a zero, 2i must be a zero, too. The "why" is beyond the scope of this response, but this result is called the "complex conjugate root theorem".
In 2., I mentioned that both -2i and 2i must be zeroes of f(x). This means that both
 and
and
 are factors of f(x), and furthermore, their product,
are factors of f(x), and furthermore, their product,
 , is also a factor. To see what's left after we factor out that product, we can use polynomial long division to find that
, is also a factor. To see what's left after we factor out that product, we can use polynomial long division to find that
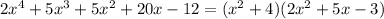
I'll go through to steps to factor that second expression below:
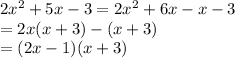
Solving both of the expressions when f(x) = 0 gets us our final two zeroes:
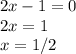

So, the remaining zeroes are 1/2 and 3.