Answer:
24. see below for a drawing with axis intercepts labeled
30. the plane is parallel to the y-z plane. It is "x=4". The only axis intercept is (4, 0, 0).
Explanation:
24. The axis intercepts are fairly easily found. You can do it a couple of ways.
first way
- Set other variables to zero and divide by the coefficient of the variable of interest.
For 3x +5y +15z = 15, the x-intercept can be found by setting y and z to zero. This gives ...
3x = 15
so, dividing by 3 tells you the x-intercept is ...
x = 15/3 = 5
Likewise, the y- and z-intercepts are, respectively, ...
y = 15/5 = 3
z = 15/15 = 1
So, the points where the plane crosses the axes are ...
(5, 0, 0), (0, 3, 0), (0, 0, 1) . . . . axes intercepts
__
second way
- Divide by the constant on the right, and express all coefficients as denominators
Doing that gives ...
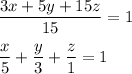
The denominators are the corresponding intercepts. (This is called the "intercept form" of the equation of the plane.)
From the above equation, we see the axis intercepts are ...
(5, 0, 0), (0, 3, 0), (0, 0, 1) . . . . same as above
Actually, the math for these two methods is virtually identical. The second way does it "all at once", so can take fewer steps. Effectively, you're doing the math of the "first way" and expressing the result in the denominator.
__
Please note that when a variable is missing, there is no intercept for that axis. That is, the plane is parallel to that axis. (In problem 30, for example, the y- and z-variables are missing. The plane x=4 is parallel to the y- and z-axes (the y-z plane).)
_____
In the first attached drawing, the x-axis is red, the y-axis is green, and the z-axis is blue. The labeling of the points is difficult to see, but the axes are a different (lighter) color behind the plane than in front of it. This plane forms a triangle in the first octant (x, y, z > 0).
In the second attached drawing, the x=0 plane is blue; the y=0 plane is green, and the z=0 plane is red. The plane of the equation is yellow. This figure better shows the triangle in the first octant.
3-D graph paper (isometric graph paper) grids are available with a web search. Such might make it easier to draw the planes you need to draw. (See the third attachment for one example.)