Question

7) P=17.59x-2655 is the profit formula for x boxes of frozen pizza dough. (By the way, what is profit?)

A) Find the profit for:
i) 10 boxes
ii) 40 “
iii) 25 “
B) How many boxes needed for
a profit of at least $700?
C) How many boxes needed to “break even”?

Answer 1

Part A)

For 10 boxes
`P=-\$2,479.10`

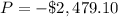
For 40 boxes
`P=-\$1,951.40`

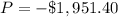
For 25 boxes
`P=-\$2,215.25`

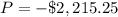
Part B) The number of boxes must be greater than or equal to 191 for a profit of at least $700

Part C) 151 boxes are needed to break even

Explanation:

we know that

Profit, is equals to revenue minus costs of goods sold

we have

`P=17.59x-2,655`

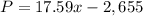
Part A) Find the profit for

1) 10 boxes

For x=10 boxes

substitute in the formula

`P=17.59(10)-2,655`

`P=-\$2,479.10`

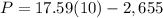
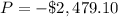
The negative means that the revenue is less than the costs

2) 40 boxes

For x=40 boxes

substitute in the formula

`P=17.59(40)-2,655`

`P=-\$1,951.40`

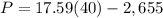
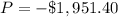
The negative means that the revenue is less than the costs

3) 40 boxes

For x=25 boxes

substitute in the formula

`P=17.59(25)-2,655`

`P=-\$2,215.25`

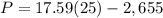
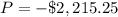
The negative means that the revenue is less than the costs

Part B) How many boxes needed for a profit of at least $700?

For P=$700

substitute in the formula and solve for x

`700=17.59x-2,655`

`17.59x=2,655+700`

`17.59x=3,355`

`x=190.7\ boxes`

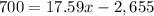
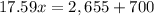
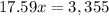
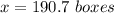
Round up

`x=191\ boxes`

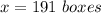
therefore

The number of boxes must be greater than or equal to 191 for a profit of at least $700

Part C) How many boxes needed to “break even”?

we know that

Break even is when the profit is equal to zero

For P=0

`0=17.59x-2,655`

`17.59x=2,655`

`x=150.9`

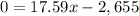
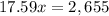
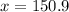
Round up

151 boxes are needed to break even