Answer:
The quadratic equation is solved .we get value of x=-3 and -1
Given data:
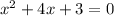
To Find:
Solve a quadratic equation:
Solution:
Step 1:
This equation is already in the form "(quadratic) equals (zero)”
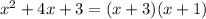
(x + 3)(x + 1) = 0
Step 2:
Now I can solve each factor by setting each one equal to zero and solving the resulting linear equations:
x + 3 = 0 or x + 1 = 0
x = –3 or x = – 1
Step 3:
These two values are the solution to the original quadratic equation. So my answer is:
x = –3, –1
Step 4:
Checking x = –3:
[–3]2 + 4[–3] + 3
9 – 12 + 3
=-3+3
=0
Step 5:
Result
Checking x = –1:
[–1]2 + 4[–1] + 3
1 – 4 + 3
-3 +3 =0
The value of x=-3 and -1