Question

A boat traveled in a river upstream for a distance of 30 miles at a constant rate, r, in miles per hour, and then made the return trip downstream at

a constant rate. If the boat took 4 hours to travel upstream and 3 hours to travel downstream, which system of equations could be used to find
the rate of the river current, c, in miles per hour?
Answer
A) 3r - 3c=30
4r + 4c = 30
B)3r + 4c = 30
3r - 4c = 30
C)4r+ 3c = 30
4r - 3c=30
D) 3r+3c = 30
4r – 4c=30
​

Answer 1

D

Explanation:

r = boat's rate

c = current's rate

1. A boat traveled in a river upstream for a distance of 30 miles. Travelling upstream, the current obstructs the movement, so the actual boat's rate is r - c mph.

If the boat took 4 hours to travel upstream, then

`(30)/(r-c)=4\\ \\4(r-c)=30\\ \\4r-4c=30`

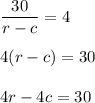
2. A boat traveled in a river downstream for a distance of 30 miles. Travelling downstream, the current helps the movement, so the actual boat's rate is r + c mph.

If the boat took 3 hours to travel downstream, then

`(30)/(r+c)=3\\ \\30=3(r+c)\\ \\3r+3c=30`

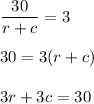
So, we get the system

4r-4c=30

3r+3c=30