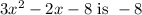Answer:
The y-intercept of y = f(x) =
 is -8.
is -8.
Solution:
From question, given equation is f(x) =

We have to find the y-intercept of the above equation
The y-intercept of the graph is the point where the function crosses the y-axis. The x-value is equal to zero for every point on the y-axis.
From question given that
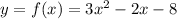 --- eqn 1
--- eqn 1
On substituting x = 0 in equation (1), the above equation becomes
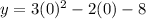
On simplifying, we get
y = 0-0-8
y = -8
So the y-intercept of f(x) =