Answer:
Two required integers are 5 and 10.
Solution:
Given that a positive integer is twice another. The sum of the reciprocals of the positive integers is
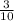
We have to find the two integers.
Let assume that one integer = x
Since another integer is twice of first one, so second integer = 2x
Reciprocal of first integer =
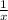
Reciprocal of first integer =
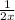
Given that sum of reciprocal =
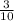
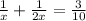
On solving above equation for x,
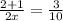
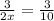
2x=10
x=5
First integer = x = 5
Second integer = 2x = 10
Hence two required integers are 5 and 10.