Question

On a trip, the fare was 50¢ for each adult and 25¢ for each child. If 30 passengers paid $12.25, how many adults and

children went?
Which of the following equations could not be used to solve the problem?
50x+ 25(30 - x) = 1225
50(30 - x + 25x = 1225
25x + 50x=30(1225)

Answer 1

The number of adult is 19 and number of children is 11

Solution:

Given that there were total 30 passengers.

Let the number of adult be x.

Therefore, number of children = 30-x

It is given that the fare for adult = 50$

The fare for x adults will be
`50 * (x)`

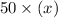
It is also given that the fare for children is 25$

The fare for (30-x) children =
`25 * (30-x)`

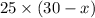
Now according to the question, 30 passengers paid $1225

50x + 25(30-x) = 1225

50x + 750 - 25x = 1225

25x = 1225-750

25x = 475

`x = (475)/(25)`

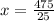
x = 19

Therefore number of adult = 19

Number of children = 30-19 = 11

From the given below equations, 25x + 50x = 30(1225) cannot be used to solve the problem.