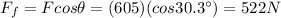Question

A mule is harnessed to a sled having a mass of 246 kg, including supplies. The mule must exert a force exceeding 1210 N at an angle of 30.3° (above the horizontal) in order to get the sled moving. Treat the sled as a point particle.

(a) Calculate the normal force (in N) on the sled when the magnitude of the applied force is 1210 N. (Enter the magnitude.) ___ N
(b) Find the coefficient of static friction between the sled and the fround beneath it. ___
(c) Find the static friction force (in N) when the mule is exerting a force of 6.05 ✕ 102 N on the sled at the same angle. (Enter the magnitude.) ___ N

Answer 1

(a) 1800 N

The equation of the forces along the vertical direction is:

`F sin \theta + N - mg = 0`

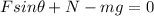
where

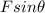`F sin \theta` is the component of the applied force along the vertical direction

N is the normal force on the sled

mg is the weight of the sled

Substituting:

F = 1210 N

m = 246 kg

`\theta = 30.3^(\circ)`

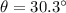
We find N:

`N=mg-F sin \theta = (246)(9.8)-(1210)(sin 30.3^(\circ))=1800 N`

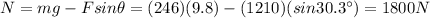
(b) 0.580

The equation of the forces along the horizontal direction is:

`F cos \theta - \mu_s N = 0`

where

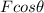`F cos \theta` is the horizontal component of the push applied by the mule

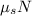`\mu_s N` is the static frictional force

Substituting:

F = 1210 N

N = 1800 N

`\theta = 30.3^(\circ)`

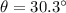
We find
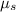`\mu_s`, the coefficient of static friction:

`\mu_s = (F cos \theta)/(N)=((1210)(cos 30.3^(\circ)))/(1800)=0.580`

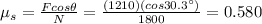
(c) 522 N

In this case, the force exerted by the mule is

`F= 6.05 \cdot 10^2 N = 605 N`

So now the equation of the forces along the horizontal direction can be written as

`F cos \theta - F_f = 0`

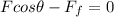
where

`\theta=30.3^(\circ)`

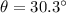
and
`F_f` is the new frictional force, which is different from part (b) (because the value of the force of friction ranges from zero to the maximum value
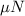`\mu N`, depending on how much force is applied in the opposite direction)

Solving the equation,

`F_f = F cos \theta = (605)(cos 30.3^(\circ))=522 N`