Step-by-step explanation:
The given data is as follows.
T =
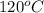 = (120 + 273.15)K = 393.15 K,
= (120 + 273.15)K = 393.15 K,
As it is given that it is an equimolar mixture of n-pentane and isopentane.
So,
 = 0.5 and
= 0.5 and
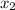 = 0.5
= 0.5
According to the Antoine data, vapor pressure of two components at 393.15 K is as follows.
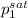 (393.15 K) = 9.2 bar
(393.15 K) = 9.2 bar
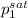 (393.15 K) = 10.5 bar
(393.15 K) = 10.5 bar
Hence, we will calculate the partial pressure of each component as follows.
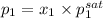
=
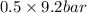
= 4.6 bar
and,
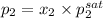
=

= 5.25 bar
Therefore, the bubble pressure will be as follows.
P =
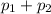
= 4.6 bar + 5.25 bar
= 9.85 bar
Now, we will calculate the vapor composition as follows.
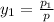
=

= 0.467
and,

=
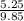
= 0.527
Calculate the dew point as follows.
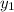 = 0.5,
= 0.5,
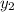 = 0.5
= 0.5

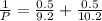
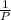 = 0.101966
= 0.101966
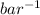
P = 9.807
Composition of the liquid phase is
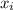 and its formula is as follows.
and its formula is as follows.

=
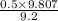
= 0.5329
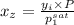
=

= 0.467