Step-by-step explanation:
We will assume that the flow rate of feed (F) = 100 g/min
(a) The overall mass balance will be as follows.
Total mass IN = Total mass OUT
as, Feed + Pure water = Product
100 + W = P
or, P - W = 100 .......... (1)
Whereas NaOH mass balance will be as follows.
Total NaOH mass IN = Total NaOH OUT
NaOH in feed + NaOH in water = NaOH in product
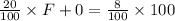
P =
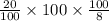
= 250 g/min
Now, we will put the value of P in equation (1) as follows.
P - W = 100
250 - W = 100
W = 250 - 100
= 150 g/min
Therefore,
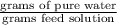 =
=
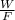
=
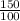
= 1.5
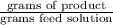 =
=
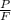
=
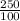
= 2.5
(b) As it is given that 8% solution (P) = 2400 lb/min.
As it is calculated that the ratio of P and F (
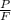 ) = 2.5
) = 2.5
So, F =
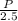
=
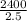
= 960 lb/min
Also,
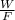 = 1.5
= 1.5
W =
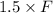
=
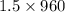
= 1440 lb/min
Therefore, we can conclude that the feed rate of 20% solution = F = 960 lb/min.
When diluted with water then W = 1440 lb/min.