Question

You want to estimate the proportion of kids between the ages of 12 and 15 who have tried marijuana. You take a random sample of 130 Maryland students and find that 23% of the sample report having tried marijuana. Last year, the federal government ran a much larger survey of 10,000 students and found that 29% reported ever using marijuana. Test the null hypothesis that the true population proportion of Maryland students who have smoked marijuana is 29% versus the alternative hypothesis that it is different than that. Use a 3% significance level. Interpret your result.

Answer 1

Answer with explanation:

Let p represents the population proportion.

By considering the given information, we have

`H_0: p=0.29\\\\H_a: p\\eq0.29`

∵ the alternative hypothesis is two tailed , so the test is two-tailed test.

Given : For sample size :n= 130,
`\hat{p}=0.23`

Test statistic:
`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}`

`z=\frac{0.23-0.29}{\sqrt{(0.29(1-0.29))/(130)}}\\\\=-1.50762993902\approx-1.51`

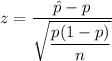
P-value (two -tailed test)=
`2P(z>|-1.51|)=0.1310434\approx 0.131`

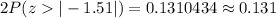
Since , the p-value (0.131) is greater than the significance level (0.03), so we accept the null hypothesis.

Thus , we conclude that we have sufficient evidence to support the null hypothesis that the true population proportion of Maryland students who have smoked marijuana is 29% .