Question

Calculate the radius of tantalum (Ta) atom, given that Ta has a BCC crystal structure, a density of 16.6 g/cm, and an atomic weight of 180.9 g/mol. (Avogadro number, 6.023 x 103 atoms/mol).

Answer 1

The radius of tantalum (Ta) atom is
`R = 1.43 * 10^(-8) \:cm = 0.143 \:nm`

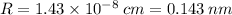
Step-by-step explanation:

From the Body-centered cubic (BBC) crystal structure we know that a unit cell length a and atomic radius R are related through

`a=(4R)/(√(3) )`

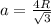
So the volume of the unit cell
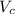`V_(c)` is

`V_(c)= a^3=((4R)/(√(3) ) )^3=(64√(3)R^3)/(9)`

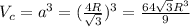
We can compute the theoretical density ρ through the following relationship

`\rho=(nA)/(V_(c)N_(a))`

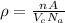
where

n = number of atoms associated with each unit cell

A = atomic weight

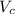`V_(c)` = volume of the unit cell

`N_(a)` = Avogadro’s number (
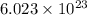`6.023 * 10^(23)` atoms/mol)

From the information given:

A = 180.9 g/mol

ρ = 16.6 g/cm^3

Since the crystal structure is BCC, n, the number of atoms per unit cell, is 2.

We can use the theoretical density ρ to find the radio R as follows:

`\rho=(nA)/(V_(c)N_(a))\\\rho=(nA)/(((64√(3)R^3)/(9))N_(a))`

Solving for R

`\rho=(nA)/(((64√(3)R^3)/(9))N_(a))\\(64√(3)R^3)/(9)=(nA)/(\rho N_(a))\\R^3=(nA)/(\rho N_(a))\cdot (1)/((64√(3))/(9)) \\R=\sqrt[3]{(nA)/(\rho N_(a))\cdot (1)/((64√(3))/(9))}`

Substitution for the various parameters into above equation yields

`R=\sqrt[3]{(2\cdot 180.9)/(16.6\cdot 6.023 * 10^(23))\cdot (1)/((64√(3))/(9))}\\R = 1.43 * 10^(-8) \:cm = 0.143 \:nm`