Question

Solve the triangle below.

Answer 1

Explanation:

Again the Law of Cosines will work here. We will first start by solving for angle C. No reason, but we have to start somewhere! The formula for the Law of Cosines in our case when solving for angle C is

`c^2=a^2+b^2-2abcosC`

Filling in with our givens:

`7^2=10^2+12^2-2(10)(12)cosC`

which simplifies a bit to

49 = 100 + 144 - 240cosC

which simplifies a bit more to

-195 = -240cosC

Divide both sides by -240 to get

.8125 = cosC

Using the inverse cosine on your calculator (the 2nd key and then the cos key will give you missing angles) you get that angle C = 35.6°

To find one more missing angle we have to use the Law of Cosines again. Let's find angle B now. Filling in the formula so it fits our needs:

`12^2=7^2+10^2-2(7)(10)cosB`

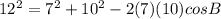
Simplifying a bit,

144 = 49 + 100 - 140cosB

which simplifies more to

-5 = -140cosB

Divide both sides by -140 to get

.0357142857 = cosB

Use the inverse cos again to find the missing angle. B = 88°, rounded from 87.9

Now we can use the Triangle Angle Sum theorem to find angle A. The theorem says that all the angles of a triangle have to add up to 180 degrees, so angle A is 56.4°, rounded.

Your answer is the second one down from the top.