Answer:
The probability is 0.000495
Explanation:
As per the question:
Total no. of cards in a deck = 52
No. of spades in a deck = 13
Now, we have to select 5 cards in a deck such that they belong to the same suit, i.e., spades.
The no. of ways of selecting 5 cards from a deck =
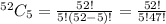
The no. of ways of selecting 5 cards from 13 spade cards =
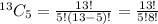
Now,
Probability that the selected 5 cards are all spades, P(E) =
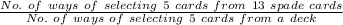
P(E) =
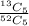
P(E) =
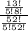
P(E) =

P(E) =
