Question

A closed-loop ecosystem is being designed for long-duration space missions. Within that system, a biofilter will utilize bacteria to convert nitrogen from fish waste (NH3) into a form usable by plants (NO3-). The biofilter consists of a cylinder filled with spherical particles (like a jar full of marbles) upon which the bacteria attach, and water then flows through the cylinder past the bacteria. The water flow rate through the system is 25 g H20 / s, and the inlet concentration of NH3in the water is 9x10-6g NH3/ g H20. If the bacteria in the filter are removing NH3at a rate of 41x10-6(g NH3)/s, what is the concentration of NH3in the outlet water, in g NH3/ g H20?

Answer 1

The concentration in the outlet water is 7.36x10-6 gNH3/gH2O

Step-by-step explanation:

We need to have the same units to do the operations so that we can substract the activity of the bacteria from the flow rate of gNH3/s for this we first need to know which is the flow of gNH3/s in the water flow rate for this we:

`25(gH2O)/(s) ((9x10^(-6)gNH3 )/(gH2O)) = 2.25x10^(-4)(gNH3)/(s)`

As you can see we used the concentration of NH3 in H2O to have the gNH3/s. Now we jst susbtract the activity of the baterias to the initial concentration of the water

`2.25(gNH3)/(s) - 41x10^(-6)(gNH3)/(s) = 1.84x10^(-4)(gNH3)/(s)`

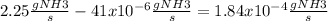
We can do this operation because the units are the same.

Now we just need to convert the 1.84x10-4 gNH3/s to concentration of gNH3/gH2O, for this we just neet to divide the concentration by the flow of the water (25gH2O/s)

`(1.84x10^(-4)(gNH3)/(s) )/(25(gH2O)/(s) ) = 7.36x10^(-6)(gNH3)/(gH2O)`

We cancel the units and when we realice the division we get that the outlet concentration of the water is 7.36x10-6gNH3/gH2O