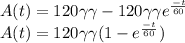Question

A tank initially contains 120L of pure water. A mixture continuing a concentration of γγ g/L of salt enters the tank at a rate of 2 L/min, and the well-stirred mixture leaves the tank at the same rate. Find an expression in terms of γγ for the amount of salt in the tank at any time tt.

Answer 1

The amount of salt in the tank at any time t is
`A(t)=120\gamma\gamma(1-e^(-t/60) )`

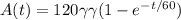
Step-by-step explanation:

By definition, we have that the change rate of salt in the tank is
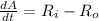`(dA)/(dt)=R_(i)-R_(o)`, where
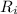`R_(i)` is the rate of salt entering and
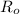`R_(o)` is the rate of salt going outside.

Then we have,
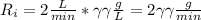`R_(i)=2(L)/(min)*\gamma\gamma(g)/(L)=2  \gamma\gamma(g)/(min)`, and

`R_(o)=2(L)/(min)*(A)/(120) (g)/(L)=(A)/(60)(g)/(min)`

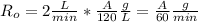
So we obtain.
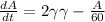`(dA)/(dt)=2  \gamma\gamma-(A)/(60)`, then

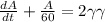`(dA)/(dt)+(A)/(60)=2  \gamma\gamma`, and using the integrating factor
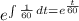`e^{\int {(1)/(60)} \, dt=e^{(t)/(60)`, therefore

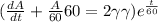`((dA )/(dt)+(A)/(60)}{60}=2  \gamma\gamma)e^{(t)/(60)`, we get
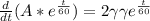`(d)/(dt)(A*e^{(t)/(60)})=  2  \gamma\gamma e^{(t)/(60)`, after integrating both sides
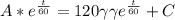`A*e^{(t)/(60)}=  120  \gamma\gamma e^{(t)/(60)}+C`, therefore
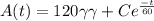`A(t)=  120  \gamma\gamma +Ce^{(-t)/(60)}`, to find
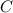`C` we know that the tank initially contains 120L of pure water, that means the initial conditions
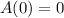`A(0)=0`, so
`0=  120  \gamma\gamma +Ce^{(-0)/(60)}`

`0=  120  \gamma\gamma +C\\C= -120  \gamma\gamma`

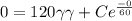
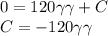
Finally we can write an expression in terms of γγ for the amount of salt in the tank at any time t, it is
`A(t)=  120  \gamma\gamma -120  \gamma\gamma e^{(-t)/(60)}\\A(t)=  120  \gamma\gamma (1-e^{(-t)/(60)})`