Question

An empty balloon is connected to a tank containing helium at 1.5 MPa and 25 °C. A valve connecting the tank and the balloon is opened until the diameter of the spherical balloon reaches a diameter of 1 m. At this point, the pressure of He inside the balloon is 500 kPa. Assuming the whole process to be isothermic, determine the minimum volume that the tank must have to inflate this balloon to its 1 m diameter

Answer 1

The minimum volume that the tank must have to inflate this balloon to its 1 m diameter is 174.53 L.

Step-by-step explanation:

Temperature of the gas = T = 25°C

Pressure of the helium gas in the tank connected to balloon =
`P_1=1.5 MPa=1.5* 10^3 kPa`

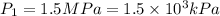
Let the minimum volume of the tank to inflate this balloon to its 1 m diameter be
`V_1`

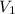
Temperature of the gas after the valve is opened = T = 25°C

Pressure inside the balloon after the valve is opened =
`P_2=500 kPa`

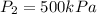
On opening the valve, helium gas starts moving towards balloon by changing its diameter to 1 m.

Diameter of balloon = d = 1 m

Volume of balloon after the valve is opened =
`V_2`

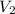
Radius of the balloon = r = d/2 = (1 m)/2 = 0.5 m

`V_2=(4)/(3)\pi r^3=(4)/(3)* 3.14* (0.5 m)^3`

`=0.5236 m^3=523 .6 L`

`1 m^3=1000 L`

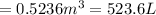
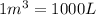
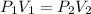`P_1V_1=P_2V_2` (Boyle's law)

`V_1=(P_2* V_2)/(P_1)`

`=(500 kPa* 523.6 L)/(1.5* 10^3 kPa)=174.53 L`

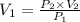
The minimum volume that the tank must have to inflate this balloon to its 1 m diameter is 174.53 L.