Question

As an aid to the establishment of personnel requirements, the director of a hospital wishes to estimate the mean number of people who are admitted to the emergency room during a 24-hour period. The director randomly selects 64 different 24-hour periods and determines the number of admissions for each. For this sample, X = 396 and S = 100. Using the sample standard deviation as an estimate for the population standard deviation, what size sample should the director choose if she wishes to estimate the mean number of admissions per 24-hour period to within 1 admission with 99% reliability?

Answer 1

n = 66.564

Explanation:

1. Because the population is unknown, we will apply the following formula to find the sample size:

`n= ((zS)/(E) )^(2)`

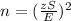
Where:

z = confidence level score.

S = standard deviation.

E = error range.

2. We will find each of these three data and replace them in the formula.

"z" theoretically is a value that measures how many standard deviations an element has to the mean. For each confidence level there is an associated z value. In the question, this level is 99%, which is equivalent to a z value of 2.58. To find this figure it is not necessary to follow any mathematical procedure, it is enough to make use of a z-score table, which shows the values ​​for any confidence interval.

The standard deviation is already provided by the question, it is S = 100.

Finally, "E" is the acceptable limit of sampling error. In the example, we can find this data. Let us note that in the end it says that the director wishes to estimate the mean number of admissions to within 1 admission, this means that she is willing to tolerate a miscalculation of just 1 admission.

Once this data is identified, we replace in the formula:

`n=(((2.58)(100))/(1) )^(2)`

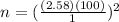
3. The corresponding mathematical operations are developed:

`n=((258)/(1) )^(2)`

`n= (258)^(2)`

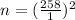
n= 66.564