Question

495 cm3 of oxygen gas at 25 oC and 114,700 Pa, and 877 cm3 of nitrogen gas 25.0 °C and 114,700 Pa, are injected into an evacuated 536 cm3 flask.

a.Find the number of moles of oxygen present prior to mixing the gases, assuming the temperature remains constant, and that oxygen is an ideal gas. (5pts)

b.Find the number of moles of nitrogen present prior to mixing the gases, assuming the temperature remains constant and that nitrogen is an ideal gas. (5pts)

c.Find the total pressure of oxygen and nitrogen in the flask (after the two gases are mixed together.

Answer 1

⇒n for oxygen = 0.0229 moles

⇒n for nitrogen = 0.0406 moles

⇒Total pressure = 2.8999 atm

Step-by-step explanation:

(a) For oxygen gas :

Given:

Pressure = 114,700 Pa

The conversion of P(Pa) to P(atm) is shown below:

`P(torr)=\frac {1}{101325}* P(atm)`

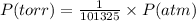
So,

Pressure = 114,700 / 101325 atm = 1.132 atm

Temperature = 25°C

The conversion of T( °C) to T(K) is shown below:

T(K) = T( °C) + 273.15

So,

T = (25 + 273.15) K = 298.15 K

T = 298.15 K

Volume = 495 cm³ = 0.495 L (1 cm³ = 1 mL = 0.001 L)

Using ideal gas equation as:

PV=nRT

where,

P is the pressure

V is the volume

n is the number of moles

T is the temperature

R is Gas constant having value = 0.0821 L.atm/K.mol

Applying the equation as:

1.132 atm × 0.495 L = n × 0.0821 L.atm/K.mol × 298.15 K

⇒n for oxygen = 0.0229 moles

(a) For nitrogen gas :

Given:

Pressure = 114,700 Pa

The conversion of P(Pa) to P(atm) is shown below:

`P(torr)=\frac {1}{101325}* P(atm)`

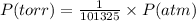
So,

Pressure = 114,700 / 101325 atm = 1.132 atm

Temperature = 25°C

The conversion of T( °C) to T(K) is shown below:

T(K) = T( °C) + 273.15

So,

T = (25 + 273.15) K = 298.15 K

T = 298.15 K

Volume = 877 cm³ = 0.877 L (1 cm³ = 1 mL = 0.001 L)

Using ideal gas equation as:

PV=nRT

where,

P is the pressure

V is the volume

n is the number of moles

T is the temperature

R is Gas constant having value = 0.0821 L.atm/K.mol

Applying the equation as:

1.132 atm × 0.877 L = n × 0.0821 L.atm/K.mol × 298.15 K

⇒n for nitrogen = 0.0406 moles

(c) For combined system :

Given:

Temperature = 25°C

The conversion of T( °C) to T(K) is shown below:

T(K) = T( °C) + 273.15

So,

T = (25 + 273.15) K = 298.15 K

T = 298.15 K

Volume = 536 cm³ = 0.536 L (1 cm³ = 1 mL = 0.001 L)

Total moles = 0.0406 moles + 0.0229 moles = 0.0635 moles

Using ideal gas equation as:

PV=nRT

where,

P is the pressure

V is the volume

n is the number of moles

T is the temperature

R is Gas constant having value = 0.0821 L.atm/K.mol

Applying the equation as:

P × 0.536 L = 0.0635 × 0.0821 L.atm/K.mol × 298.15 K

⇒Total pressure = 2.8999 atm