Answer:
V=15.46m/s
Step-by-step explanation:
By making an energy balance:
Initial energy:
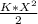 where K=1100N/m and X=4m
where K=1100N/m and X=4m
Final energy:
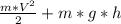 where m=60kg and h=2.5m
where m=60kg and h=2.5m
Work done by friction force: -Ff*X where Ff = 40N and X=4m
The balance will be:
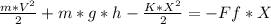 Solving for V:
Solving for V:
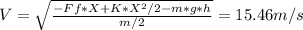 using g=9.8m/s^2
using g=9.8m/s^2