Question

Wool Express (WE) has a capital structure of 30% debt and 70% equity. WE is considering a project that requires an investment of$2.6 million. To finance this project, WE plans to issue 10-year bonds with a coupon interest rate of 12%. Each of these bonds has a $1,000 face value and will be sold to net WE $980. If the current risk-free rate is 7% and the expected market return is 14.5%, what is the weighted cost of capital for WE? Assume WE has a beta of 1.20 and a marginal tax rate of 40%.

Answer 1

13.41%

Step-by-step explanation:

Given:

Weight of debt =30% ; Weight of equity =70%; Coupon rate =12%

Risk-free rate,
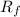`R_(f)` =7% ; Expected market rate,
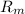`R_(m)`=14.5% ; Beta,
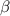`\beta`= 1.20; Tax-Rate,
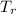`T_(r)`=40%

We can calculate the following thus;

Return on bond =
`(Coupon Interest)/(Sales price of the bond) =(0.12*1000)/(980)=(120)/(980) = 12.24`%

Cost of debt =Return on bond *(1-
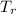`T_(r)`)=12.24% *(1-0.4)

=12.24%*0.6 = 7.35%

To compute the cost of equity capital
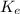`K_(e)`, we shall use the CAPM formula below

`K_(e) =R_(f) +\beta (R_(m) - R_(f) )`

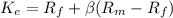
= 7% + 1.2(14.5%-7.0%)

= 7% +1.20( 7.5%) = 7% + 9% = 16%

The Weighted Average Cost of Capital, WACC is worked out as

WACC= (Weight of debt*Cost of debt) + (Weight of equity *Cost of equity)

= (30% *7.35) +(70% *16)

= 13.405

= 13.41%