Question

Calculate the activity coefficients for the following conditions:

a.Cu2+ in a 0.01 M NaCl solution

b.K+in a 0.025M HCl solution

c.K+in a 0.02 K2SO4 solution

Answer 1

For a: The activity coefficient of copper ions is 0.676

For b: The activity coefficient of potassium ions is 0.851

For c: The activity coefficient of potassium ions is 0.794

Step-by-step explanation:

To calculate the activity coefficient of an ion, we use the equation given by Debye and Huckel, which is:

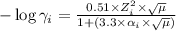`-\log\gamma_i=(0.51* Z_i^2* √(\mu))/(1+(3.3* \alpha _i* √(\mu)))` ........(1)

where,

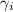`\gamma_i` = activity coefficient of ion

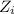`Z_i` = charge of the ion

`\mu` = ionic strength of solution

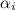`\alpha _i` = diameter of the ion in nm

To calculate the ionic strength, we use the equation:

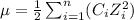`\mu=(1)/(2)\sum_(i=1)^n(C_iZ_i^2)` ......(2)

where,

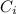`C_i` = concentration of i-th ions

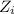`Z_i` = charge of i-th ions

• For a:

We are given:

0.01 M NaCl solution:

Calculating the ionic strength by using equation 2:

`C_(Na^+)=0.01M\\Z_(Na^+)=+1\\C_(Cl^-)=0.01M\\Z_(Cl^-)=-1`

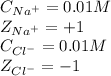
Putting values in equation 2, we get:

`\mu=(1)/(2)[(0.01* (+1)^2)+(0.01* (-1)^2)]\\\\\mu=0.01M`

Now, calculating the activity coefficient of
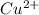`Cu^(2+)` ion in the solution by using equation 1:

`Z_(Cu^(2+))=2+\\\alpha_(Cu^(2+))=0.6\text{  (known)}\\\mu=0.01M`

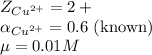
Putting values in equation 1, we get:

`-\log\gamma_(Cu^(2+))=(0.51* (+2)^2* √(0.01))/(1+(3.3* 0.6* √(0.01)))\\\\-\log\gamma_(Cu^(2+))=0.17\\\\\gamma_(Cu^(2+))=10^(-0.17)\\\\\gamma_(Cu^(2+))=0.676`

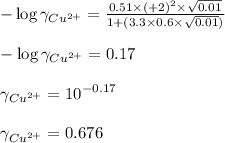
Hence, the activity coefficient of copper ions is 0.676

• For b:

We are given:

0.025 M HCl solution:

Calculating the ionic strength by using equation 2:

`C_(H^+)=0.025M\\Z_(H^+)=+1\\C_(Cl^-)=0.025M\\Z_(Cl^-)=-1`

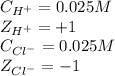
Putting values in equation 2, we get:

`\mu=(1)/(2)[(0.025* (+1)^2)+(0.025* (-1)^2)]\\\\\mu=0.025M`

Now, calculating the activity coefficient of
`K^(+)` ion in the solution by using equation 1:

`Z_(K^(+))=+1\\\alpha_(K^(+))=0.3\text{  (known)}\\\mu=0.025M`

Putting values in equation 1, we get:

`-\log\gamma_(K^(+))=(0.51* (+1)^2* √(0.025))/(1+(3.3* 0.3* √(0.025)))\\\\-\log\gamma_(K^(+))=0.070\\\\\gamma_(K^(+))=10^(-0.070)\\\\\gamma_(K^(+))=0.851`

Hence, the activity coefficient of potassium ions is 0.851

• For c:

We are given:

0.02 M
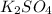`K_2SO_4` solution:

Calculating the ionic strength by using equation 2:

`C_(K^+)=(2* 0.02)=0.04M\\Z_(K^+)=+1\\C_(SO_4^(2-))=0.02M\\Z_(SO_4^(2-))=-2`

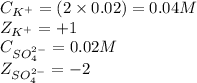
Putting values in equation 2, we get:

`\mu=(1)/(2)[(0.04* (+1)^2)+(0.02* (-2)^2)]\\\\\mu=0.06M`

Now, calculating the activity coefficient of
`K^(+)` ion in the solution by using equation 1:

`Z_(K^(+))=+1\\\alpha_(K^(+))=0.3\text{  (known)}\\\mu=0.06M`

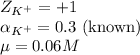
Putting values in equation 1, we get:

`-\log\gamma_(K^(+))=(0.51* (+1)^2* √(0.06))/(1+(3.3* 0.3* √(0.06)))\\\\-\log\gamma_(K^(+))=0.1\\\\\gamma_(K^(+))=10^(-0.1)\\\\\gamma_(K^(+))=0.794`

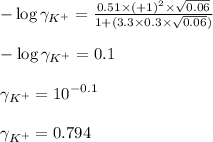
Hence, the activity coefficient of potassium ions is 0.794