Answer with explanation:
Let p represents the population proportion.
Then According to the given information, we have
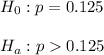
∵ the alternative hypothesis is right-tailed , so the test is right-tailed test.
Given : For sample size of n=410 U.S. workers is collected in 2006 , 50 of the workers belonged to unions.
Then , sample proportion :
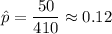 [Rounded to 2 decimals]
[Rounded to 2 decimals]
Test statistic:
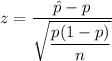
 [Rounded to 2 decimals]
[Rounded to 2 decimals]
The value of the test statistic : z= -0.31
P-value (Right -tailed test)=
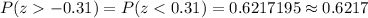 [Rounded to 4 decimals]
[Rounded to 4 decimals]
Since , the p-value (0.6217) is greater than the significance level (0.05), so we accept the null hypothesis.
Conclusion: We have sufficient evidence to reject the alternative hypothesis that the union membership increased in 2006.