Question

A new test has been devised for detecting a particular type of cancer. If the test is applied to a person who has this type of cancer, the probability that the person will have a positive reaction is 0.95 and the probability that the person will have a negative reaction is 0.05. If the test is applied to a person who does not have this type of cancer, the probability that the person will have a positive reaction is 0.05 and the probability that the person will have a negative reaction is 0.95. Suppose that in the general population, one person out of every 100,000 people has this type of cancer. If a person selected at random has a positive reaction to the test, what is the probability that he has this type of cancer?

Answer 1

0.000189

Explanation:

Given:

Probability of positive reaction given that he has cancer, P(p/c) = 0.95

Probability of negative reaction given that he has cancer, P(n/c) = 0.05

Probability of positive reaction given that not having cancer, P(p/c') = 0.05

Probability of negative reaction given that not having cancer, P(n/c') = 0.95

Probability that the person has particular type of cancer,

P(C) =
`\frac{\textup{1}}{\textup{100,000}}=0.00001`

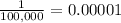
Probability that the person does not has particular type of cancer,

P(C') = 1 - 0.00001 = 0.99999

Now,

Using the Baye's Theorem

Probability that the person selected at random has a positive reaction to the test, that he has this type of cancer

=
`(P(p/c)* P(C))/(P(p/c)* P(C)+P(p/c')* P(C'))`

=
`(0.95*0.00001)/(0.95*0.00001+0.05*0.99999)`

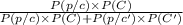
= 0.000189