Question

A brass alloy is known to have a yield strength of 240 MPa (35,000 psi), a tensile strength of 310 MPa (45,000 psi), and an elastic modulus of 110 GPa (16.0 * 106 psi). A cylindrical specimen of this alloy 15.2 mm (0.60 in.) in diameter and 380 mm (15.0 in.) long is stressed in tension and found to elongate 1.9 mm (0.075 in.). On the basis of the information given, is it possible to compute the magnitude of the load necessary to produce this change in length? If so, calculate the load; if not, explain why.

Answer 1

Here Strain due to testing is greater than the strain due to yielding that is why computation of load is not possible.

Step-by-step explanation:

Given that

Yield strength ,Sy= 240 MPa

Tensile strength = 310 MPa

Elastic modulus ,E= 110 GPa

L=380 mm

ΔL = 1.9 mm

Lets find strain:

Case 1 :

Strain due to elongation (testing)

ε = ΔL/L

ε = 1.9/380

ε = 0.005

Case 2 :

Strain due to yielding

`\varepsilon' =(S_y)/(E)`

`\varepsilon' =(240)/(110* 1000)`

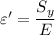
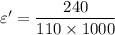
ε '=0.0021

Here Strain due to testing is greater than the strain due to yielding that is why computation of load is not possible.

For computation of load strain due to testing should be less than the strain due to yielding.