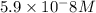Answer:
For a:
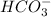 will dominate at pH = 9.1
will dominate at pH = 9.1
For b: The concentration of carbonate ions at pH = 9.1 will be
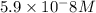
Step-by-step explanation:
To calculate the pH of the solution, we use the equation:
![pH=-\log[H^+]](https://img.qammunity.org/2020/formulas/chemistry/middle-school/vz65x0ueuj8r8ibqa81zvsbzb2yaetlce4.png) ......(1)
......(1)
We are given:
pH = 9.1
Putting values in equation 1, we get:
![9.1=-\log[H^+]](https://img.qammunity.org/2020/formulas/chemistry/college/2koh1bgqwqbk6cw5owavcqzid3b7480ewl.png)
![[H^+]=10^(-9.1)](https://img.qammunity.org/2020/formulas/chemistry/college/fnjqhyzennufpcobzipyxb6vbzs7e7jehl.png)
For the given chemical equation:
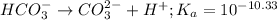
The expression of
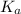 for above reaction follows:
for above reaction follows:
![K_a=([CO_3^(2-)]* [H^+])/([HCO_3^-])](https://img.qammunity.org/2020/formulas/chemistry/college/9wfiig6h47rspx1scooh742lciuuj9brmn.png)
Putting value of hydrogen ion concentration in above equation, we get:
![10^(-10.33)=([CO_3^(2-)]* 10^(-9.1))/([HCO_3^-])\\\\([HCO_3^-])/([CO_3^(2-)])=(10^(-9.1))/(10^(-10.33))\\\\([HCO_3^-])/([CO_3^(2-)])=16.98](https://img.qammunity.org/2020/formulas/chemistry/college/kydigdic1erm93wvrtp6z98n77vs5wyj9z.png)
![[HCO_3^-]=16.98* [CO_3^(2-)]](https://img.qammunity.org/2020/formulas/chemistry/college/5cpl3gu5blcyjkunyzk3ockg9wxr9dshp8.png)
Hence,
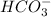 will dominate at pH = 9.1
will dominate at pH = 9.1
The expression of
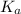 for above reaction follows:
for above reaction follows:
![K_a=([CO_3^(2-)]* [H^+])/([HCO_3^-])](https://img.qammunity.org/2020/formulas/chemistry/college/9wfiig6h47rspx1scooh742lciuuj9brmn.png)
We are given:
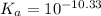
![[H^+]=10^(-9.1)](https://img.qammunity.org/2020/formulas/chemistry/college/fnjqhyzennufpcobzipyxb6vbzs7e7jehl.png)
![[HCO_3^-]=10^(-6)M](https://img.qammunity.org/2020/formulas/chemistry/college/cl6hfwc9v02ci5qadrxft9dc0ojgpc8ehc.png)
Putting values in above equation, we get:
![10^(-10.33)=([CO_3^(2-)]* 10^(-9.1))/(10^(-6))](https://img.qammunity.org/2020/formulas/chemistry/college/i9g6zfatq9u3697c4jui5ctztuabbh1km8.png)
![[CO_3^(2-)]=(10^(-6)* 10^(-10.33))/(10^(-9.1))=5.9* 10^-8}M](https://img.qammunity.org/2020/formulas/chemistry/college/qtj5r31p9x4ld7gm8sc8q02vkfw2hklri4.png)
Hence, the concentration of carbonate ions at pH = 9.1 will be