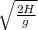Question

A stone is thrown horizontally from the top of a cliff and eventually hits the ground below. A second stone is dropped from rest from the same cliff, falls through the same height, and also hits the ground below. Ignore air resistance. Discuss whether each of the following quantities is different or the same in the two cases; if there is a difference, describe the difference:

(a) displacement.
(b) speed just before impact with the ground, and
(c) time of flig

Answer 1

Answer and Explanation:

As per the question:

When the stone is thrown from the cliff top and hits the ground below eventually:

R =
`v_(o)\sqrt{(2H)/(g)}`

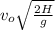
where

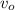`v_(o)` = initial velocity

H = height

g = acceleration due to gravity

R = horizontal Range

Now,

(a) Displacement of the stone is given by the horizontal range:

R =
`v_(o)\sqrt{(2H)/(g)}`

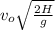
where

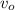`v_(o)` = initial velocity

H = height

g = acceleration due to gravity

R = horizontal Range

(b) Speed just prior to the impact is given by the third equation of motion:

`v = \sqrt{v_(o)^(2) + 2gH}`

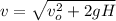
where

v = final velocity

(c) Time of flight is given by the second eqn of motion where the initial velocity is considered to be 0 then:

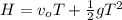
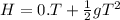
`H = v_(o)T + (1)/(2)gT^(2)`

`H = 0.T + (1)/(2)gT^(2)`

T =
`\sqrt{(2H)/(g)`