Question

A ball is dropped from a height of 1.00 m above the floor. Each time it bounces, it rebounds to 1/2 the maximum height it had in the previous bounce. Starting from the time the ball is first released, how much time elapses until the ball stops bouncing?

Answer 1

the ball bounces during 2.633s.

Step-by-step explanation:

using the equations of free fall movement and considering that the ball has no initial speed we have:

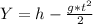`Y=h-(g*t^(2) )/(2)` where h=1m, g=9.8m/
`s^(2)`.

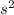equaling Y to zero to find the time we have:

`0=h-(g*t^(2) )/(2)`

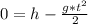
and then:

`t=\sqrt{(2h)/(g) }`

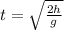
so this is the time that elapsed since the ball was dropped untill it hits the floor the first time, from here on we use the fact that the time to go up is the same time to go down since the heigth of release and arrive is the same, so the time for the next bounce is:

`t=\sqrt{(2(h/2))/(g) }`

and for the next one:

[
`t=\sqrt{(2(h/4))/(g) }`

and so on, so the total time will be an infinty serie, which will look like this:

`t=\sqrt{(2)/(g)*h }+2\sqrt{(2)/(g)*(h)/(2)}+2\sqrt{(2)/(g)*(h)/(4)}+2\sqrt{(2)/(g)*(h)/(8)}...`

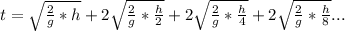
factorizing, and replacing the value of h we have:

`t=\sqrt{(2)/(g) }(1+2*\sqrt{(1)/(2) }+2*\sqrt{(1)/(2) } ^(2)+2*\sqrt{(1)/(2) } ^(3)+... )`

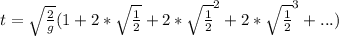
here we have to write 1=2-1 to complete the serie:

`t=\sqrt{(2)/(g) }(-1+2*\sqrt{(1)/(2) } ^(0)+2**\sqrt{(1)/(2) } ^(1)+2*\sqrt{(1)/(2) } ^(2)+2*\sqrt{(1)/(2) } ^(3)+... )`

and this is a geometric serie, of the form sum from n=0 to n=infinity of
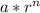`a*r^(n)` where a=2 and
`r=\sqrt{(1)/(2) }`.

The solution for this serie is well known and it is
`(a)/(1-r)`

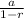
which gives:
`(a)/(1-r)=\frac{2}{1-\sqrt{(1)/(2) } }=6.828`

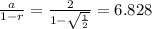
and replacing this we have:

`t=\sqrt{(2)/(g) }(-1+6.828 )`

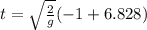
replacing g and solving:

`t=\sqrt{(2)/(9.8) }(5.828 )=2.633s`

the units of time are seconds because the gravitational aceleration is in
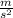`(m)/(s^(2) )` the meters cancelled with the meters of the h and the square of the second is gone because of the square root.